Конденсатор

Схема замещения не идеального (реального) конденсатора:

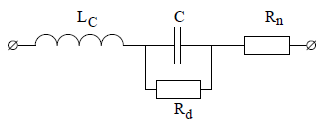
При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый емкостью C, собственной индуктивностью L_C и сопротивлением потерь R_п.

Сопротивление потерь — эквивалентное последовательное сопротивление (ЭПС (англ. ESR), внутреннее сопротивление), обусловлено, главным образом, электрическим сопротивлением материала обкладок и выводов конденсатора и контактов между ними, а также учитывает потери в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор, вследствие поверхностного эффекта (скин-эффекта). Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].

В большинстве практических случаев этим параметром можно пренебречь, но, иногда (например, в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания), достаточно малое его значение существенно для надежности и устойчивости работы устройства. В электролитических конденсаторах, где один из электродов является электролитом, этот параметр при эксплуатации со временем деградирует, вследствие испарения растворителя из жидкого электролита и изменения его химического состава, вызванного взаимодействием с металлическими обкладками, что происходит относительно быстро в низкокачественных изделиях.

Некоторые схемы (например, стабилизаторы напряжения) критичны к диапазону изменения ЭПС конденсаторов в своих цепях. Это связано с тем, что при проектировании таких устройств инженеры учитывают этот параметр в фазочастотной характеристике (ФЧХ) обратной связи стабилизатора. Существенное изменение со временем ЭПС примененных конденсаторов изменяет ФЧХ, что может привести к снижению запаса устойчивости контуров авторегулирования, и, даже, к самовозбуждению.

Существуют специальные приборы (англ. ESR-метр) для измерения этого достаточно важного параметра конденсатора, по которому можно часто определить пригодность его дальнейшего использования в определенных целях. Этот параметр, кроме собственно емкости — часто имеет решающее значение в исследовании состояния старого конденсатора и принятия решения, стоит ли использовать его в определенной схеме, или он прогнозируемо выйдет за пределы допустимых отклонений.

Собственная индуктивность — эквивалентная последовательная индуктивность (ЭПИ (англ. ESL)), обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. Результатом этой распределенной паразитной индуктивности является превращение конденсатора в колебательный контур с характерной собственной частотой резонанса. Эта частота может быть измерена и обычно указывается в параметрах конденсатора либо в явном виде, либо в виде рекомендованной максимальной рабочей частоты.

Резонансная частота конденсатора:

${{f}_{p}}=\frac{1}{2\pi \sqrt{{{L}_{c}}C}}.$

При f > f_р конденсатор в цепи переменного тока ведет себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f < f_p, на которых его сопротивление носит емкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Энергия заряженного конденсатора:

$\displaystyle W=\frac{C{{U}^{2}}}{2}=\frac{qU}{2}=\frac{{{q}^{2}}}{2C}\text{,}$

где:

U — напряжение (разность потенциалов) на обкладках конденсатора;

q – величина накопленного электрического заряда;

С – емкость конденсатора.

Несколько явлений, напрямую связанных с физикой диэлектриков:

Спойлер

Тангенс угла диэлектрических потерь:

Так как реальные среды анизотропные и неоднородные, диэлектрическая проницаемость будет иметь комплексный вид:

$\dot{\varepsilon }={{\varepsilon }_{a}}+j\frac{\gamma }{\omega }\text{,}$

${{\varepsilon }_{a}}=\varepsilon {{\varepsilon }_{0}}\text{.}$

Тангенс угла диэлектрических потерь выражается отношением мнимой и вещественной части комплексной диэлектрической проницаемости:

$tg\delta =\frac{\gamma }{\omega \text{ }{{\varepsilon }_{a}}}\text{.}$

где:

γ – проводимость среды;

ω – частота колебаний;

ε_а – абсолютная диэлектрическая проницаемость.

Очевидно, что у идеального диэлектрика проводимость γ→0, следовательно, тангенс угла потерь показывает степень отличия реального диэлектрика от идеального.

Электрическое сопротивление изоляции диэлектрика конденсатора R_d, ток утечки и саморазряд:

Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением ${{R}_{d}}=\frac{U}{{{I}_{leak.}}}$ , где: U — напряжение, приложенное к конденсатору, I_leak. — ток утечки.

Из-за тока утечки, протекающего через слой диэлектрика между обкладками и по поверхности диэлектрика, предварительно заряженный конденсатор с течением времени теряет заряд (саморазряд конденсатора). Часто, в спецификациях на конденсаторы, сопротивление утечки определяют через постоянную времени τ саморазряда конденсатора, которая численно равна произведению емкости на сопротивление утечки:

$\tau ={{R}_{d}}\cdot C\text{.}$

τ — это время, за которое начальное напряжение на конденсаторе, неподключенном к внешней цепи уменьшится в e раз.

Хорошие конденсаторы с полимерными и керамическими диэлектриками имеют постоянные времени саморазряда достигающие многих сотен тысяч часов.

Диэлектрическая абсорбция:

Если заряженный конденсатор быстро разрядить до нулевого напряжения путем подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то можно увидеть, что напряжение на обкладках снова появится, как если бы конденсатор разрядили не до нуля. Это явление получило название диэлектрическая абсорбция (диэлектрическое поглощение). Конденсатор ведет себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора.

Подобный эффект можно наблюдать практически на всех типах диэлектриков. В электролитических конденсаторах он особенно ярок и является следствием химических реакций между электролитом и обкладками. У конденсаторов с твердым диэлектриком (например, керамических и слюдяных) эффект связан с остаточной поляризацией диэлектрика. Наименьшим диэлектрическим поглощением обладают конденсаторы с неполярными диэлектриками: тефлон (фторопласт), полистирол, полипропилен и т. п.

Эффект зависит от времени зарядки конденсатора, времени закорочения, иногда от температуры. Количественное значение абсорбции принято характеризовать коэффициентом абсорбции, который определяется в стандартных условиях.

Паразитный пьезоэффект:

Многие керамические материалы, используемые в качестве диэлектрика в конденсаторах (например, титанат бария, обладающий очень высокой диэлектрической проницаемостью в не слишком сильных электрических полях) проявляют пьезоэффект — способность генерировать напряжение на обкладках при механических деформациях. Это характерно для конденсаторов с пьезоэлектрическими диэлектриками. Пьезоэффект ведет к возникновению электрических помех, в устройствах, где использованы такие конденсаторы при воздействии акустического шума или вибрации на конденсатор. Это нежелательное явление иногда называют («микрофонным эффектом»).

Также, подобные диэлектрики проявляют и обратный пьезоэффект — при работе в цепи переменного напряжения происходит знакопеременная деформация диэлектрика, генерирующая акустические колебания, порождающие дополнительные электрические потери в конденсаторе.

Самовосстановление:

Конденсаторы с металлизированным электродом (бумажный и пленочный диэлектрик) обладают важным свойством самовосстановления (англ. self-healing, cleaning) электрической прочности после пробоя диэлектрика. Механизм самовосстановления заключается в отгорании металлизации электрода после локального пробоя диэлектрика посредством микродугового электрического разряда.

Страниц: 1 2 3 4 5 6