Электронно-дырочный p-n переход
На практике используются контакты: полупроводник-полупроводник, полупроводник — металл, металл — диэлектрик — полупроводник.
Переход между двумя областями полупроводника с разнотипной проводимостью называется электронно-дырочным переходом или p-n переходом.
Переходы между двумя областями с различной концентрацией примесей одного типа называют электронно-электронными (n+ — n переход) или дырочно-дырочным (p+ — p), знак «+» означает повышенную концентрацию примесей по сравнению со вторым слоем.
Переходы между двумя полупроводниковыми материалами, имеющими различную ширину запрещенной зоны, называют гетеропереходами. Если одна из областей, образующих переход, является металлом, то такой электрический переход называют переходом металл — полупроводник.
Концентрации основных носителей заряда в p-n переходе могут быть равными или значительно различаться. Электронно-дырочный переход, у которого pp ≈ np, называется симметричным.
Если концентрации основных носителей наряда в областях различны (nn ≫ pp или pp ≫ nn) и отличаются на два-три порядка, то p-n переходы называют несимметричными. Такие переходы на практике используются чаще, чем симметричные.
В зависимости от характера распределения примесей различают две разновидности переходов: резкий (ступенчатый) и плавный. При резком переходе концентрации примесей на границе раздела областей изменяются на расстоянии, соизмеримом с диффузионной длиной, а при плавном— на расстоянии, значительно большем диффузионной длины.
p—n переход в состоянии равновесия
Прежде всего, необходимо сказать, что данные рассуждения действительны при условии, что:
1) на границе раздела p- и n — областей отсутствуют механические дефекты и включения других химических веществ;
2) при комнатной температуре все атомы примеси ионизированы, т.е. pp = Nа, nn = Nд;
3) на границе p-n перехода тип примеси резко изменяется.
Поскольку концентрация электронов в n-области намного больше их концентрации в р-области, а концентрация дырок в р-области намного больше, чем в n-области (nn ≫ np, pp ≫ pn), то на границе раздела полупроводников возникает градиент (перепад) концентрации подвижных носителей заряда (дырок и электронов): ![]()
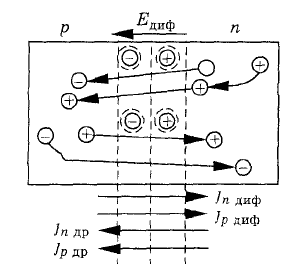
Под его действием заряды будут диффундировать из области с более высокой концентрацией в область с пониженной концентрацией. Направленное движение свободных носителей, вызванное их неравномерным распределением в объеме полупроводника, называют диффузионным движением. Электроны под действием диффузии перемешаются из n-области в p-область, а дырки перемещаются из p-области в n-область. Это движение зарядов (основных носителей) образует диффузионный ток p-n перехода, содержащий две составляющие: электронную и дырочную, плотность которых определяется из соотношений:
![]()
![]()
где:
![]() — градиенты концентраций электронов и дырок соответственно;
— градиенты концентраций электронов и дырок соответственно;
Dn и Dp – коэффициенты диффузии электронов и дырок соответственно;
q – заряд электрона.
Коэффициент диффузии показывает количество носителей заряда, пересекающих в единицу времени единичную площадку, перпендикулярную к выбранному направлению, при величине градиента концентрации в этом направлении, равном единице.
В результате протекания диффузионного тока граничный слой обедняется подвижными носителями заряда. В приконтактной области n-типа появляется нескомпенсированный малоподвижный положительный заряд за счет ионов донорной примеси, а в р-области — отрицательный заряд за счет ионов акцепторной примеси.
Таким образом, на границе p- и n-областей возникает двойной слой объемного пространственного заряда, наличие которого приводит к образованию электрического поля, напряженность которого равна Eдиф. Это поле препятствует дальнейшему протеканию диффузионного тока (тока основных носителей). Поскольку обедненный слой обладает малой электропроводностью (в нем практически отсутствуют подвижные носители заряда), то он называется запирающим слоем или областью объемного заряда.
В n- и р-областях полупроводника, кроме основных носителей, существуют неосновные: дырки в n-области и электроны в р-области. Неосновные носители совершают тепловое движение (дрейф) и перемещаются к запирающему слою p-n перехода. Их перемещение характеризуется подвижностью µ. Подвижность равна средней скорости ![]() , приобретаемой носителями заряда в направлении действия электрического поля с напряженностью E = 1 В/м:
, приобретаемой носителями заряда в направлении действия электрического поля с напряженностью E = 1 В/м:
![]()
Поле p-n перехода является ускоряющим для неосновных носителей заряда. Электроны (неосновные носители р-области), подойдя к переходу, подхватываются электрическим полем и перебрасываются в n-область, а дырки n-области — в р-область. Дрейф неосновных носителей вызывает появление электронной и дырочной составляющих тока дрейфа, плотность которых определяется из соотношений:
![]()
![]()
где:
n, p – количество электронов и дырок соответственно.
Полная плотность тока дрейфа (тепловой ток):
![]()
Если вспомнить вид закона Ома в дифференциальной форме (если воспоминания даются тяжело, то: ![]() ), то можно легко заметить, что удельная проводимость полупроводника определяется соотношением:
), то можно легко заметить, что удельная проводимость полупроводника определяется соотношением:
![]()
При комнатной температуре некоторое количество основных носителей заряда обладает энергией, достаточной для преодоления поля запирающего слоя, и протекает незначительный диффузионный ток. Этот ток уравновешивается дрейфовым током. Поэтому при отсутствии внешнего поля в p-n переходе устанавливается термодинамическое равновесие токов. Ток диффузии уравновешивается (компенсируется) дрейфовым током:
![]()
Не равномерность концентрации носителей зарядов в полупроводнике возникает при воздействии внешних управляющих факторов: электрического поля, нагревания, освещения и др. Равновесие концентраций электронов и дырок в полупроводнике нарушается и появляется дополнительная неравновесная концентрация носителей заряда. После прекращения внешнего воздействия происходит процесс рекомбинации электронов и дырок. Полупроводник переходит в равновесное состояние.
Контактная разность потенциалов
Вы наверняка уже заметили, что раз у нас есть области с противоположными по знаку зарядами, то должно присутствовать какое-то напряжение. Это напряжение называется контактной разностью потенциалов Uк, и составляет: для кремния (Si) — Uк = 0.9-1.2 В; для германия (Ge) — Uк = 0.6-0.7 В.
Величина контактной разности потенциалов (потенциального барьера) определяется положением уровней Ферми в областях n- и p-типа:
![]()
Для нахождения аналитического выражения контактной разности потенциалов можно воспользоваться условием равновесного состояния p-n перехода, и соотношением Эйнштейна для коэффициента диффузии и подвижности носителей заряда:
![]()
![]()
![]()
где:
![]() — тепловой потенциал (е – элементарный заряд электрона, k – постоянная Больцмана, Т – абсолютная температура);
— тепловой потенциал (е – элементарный заряд электрона, k – постоянная Больцмана, Т – абсолютная температура);
В результате получается:
![]()
![]()
Отсюда следует, что контактная разность потенциалов зависит:
1) от ширины запрещенной зоны полупроводника. При одинаковых концентрациях примесей она выше у полупроводников с большей шириной запрещенной зоны;
2) от концентрации примесей в смежных областях полупроводника. При их увеличении контактная разность потенциалов возрастает;
3) от температуры полупроводника. При ее увеличении контактная разность потенциалов уменьшается.
Толщина p-n перехода также будет зависеть от концентрации примесей:
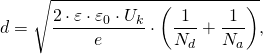
где:
![]() — контактная разность потенциалов;
— контактная разность потенциалов;
![]() — относительная диэлектрическая проницаемость материала и вакуума соответственно;
— относительная диэлектрическая проницаемость материала и вакуума соответственно;
![]() — заряд электрона;
— заряд электрона;
![]() — концентрации донорной и акцепторной примесей соответственно.
— концентрации донорной и акцепторной примесей соответственно.